This tweet sums up today’s class.
We’ve had a two week break, culminating with a public holiday Monday. In our first class back, I wanted to add some supporting activities for the difficulties we were having in our last class. Let’s just say that I’m not sure that what we did today helped! Luckily, I have another opportunity with the other half of the class tomorrow. I thought I’d write a blog post to help organise my thoughts (and provide some kind of detailed post-class lesson plan), and then press send so that others can have a peek into my thought process (for what it’s worth!), and perhaps offer suggestions. If you want to focus on what didn’t work so well, skip right to the last section.
Previously …
We’ve been developing mathematical reasoning using the key elements of noticing patterns, conjecturing and generalising, crafting claims, and exploring why (proving). (I’ve leant quite heavily in places on Chapter 10 of Tracy Zager’s Becoming the Math Teacher You Wish You’d Had for what follows.)
In our last class (before the break), we were working on claims. For each claim, I asked students to think about whether the statement is true, and, if so, when the statement is true. To help with this, I asked students to find counterexamples (examples where the claim doesn’t hold true). Then, they needed to revise the conditions of the claim to make it always true.
For example: ‘If you subtract a number from 5, your answer will be less than or equal to 5.’ This is definitely not always true. A counterexample is -7; if we subtract -7 from 5, the answer is 12, which is not less than or equal to 5. With some more investigation we can see that this statement is always true if we revise the conditions on the claim to be ‘for all numbers greater than or equal to zero’.
Here are some of the others that students worked on:
- A rectangle is a square.
- The sum of four even numbers is divisible by 4.
- One-third is one of three pieces.
- An even number divided by an even number is an even number.
- Division always makes a number smaller.
- The square of a number is greater than or equal to the number.
- When you add two numbers you get the same result as when you multiply them.
These kinds of statements are used in the instructional routine Always, Sometimes, Never. For more on this, I thoroughly recommend Chapter 10 of Tracy’s book. If you don’t have access to the book, you can still check out the links at the companion website.
Of the wide variety of statements, students struggled (perhaps most) with the nature of statements 2 and 4. The discussion around ‘A rectangle is a square’ led me to think that our experience with classifying objects (in particular, shapes) and identifying properties they had in common needed to be richer. Which led me to the plans for today’s class …
Today’s class
If I’m honest, I kind of skirt around geometry, in particular the properties of shapes — too many definitions that differ depending on which part of the world you are from. But shapes offer lots of opportunities for classifying and characterising, and for nailing down some precise terminology. So, I started by sharing in a matter-of-fact way that I was a little uneasy with what we were about to do but that, as teachers, we can’t simply avoid a topic.
The progression that follows includes ideas from Pauline Carter and Kath Ireland, as well as from Van de Walle et al. (2018) Teaching Student-Centred Mathematics Vol III (Grades 6-8). Underlying all of this are the Van Hiele levels of geometric thought. I won’t elaborate, but a Google search should help — and Christopher Danielson’s excellent Teacher Guide for his Which One Doesn’t Belong? book gave me a useful way to describe the different levels to my pre-service teachers at the end of the session.
1. Names of shapes
I gave this handout and asked students to name as many of the shapes as they could. (I chose not to pre-cut shapes for the students so that orientation was initially fixed.) The purpose of talking about the shapes was to draw out some terminology and some misconceptions. For example, we talked about ‘diamonds’ and the orientation of shapes. We talked about concave and convex. But, I refused to arbitrate on the precise names of shapes at this stage — that was for them to determine!
We kept this page up throughout the workshop, and added notation for parallel sides, congruent sides, right angles,and congruent angles.

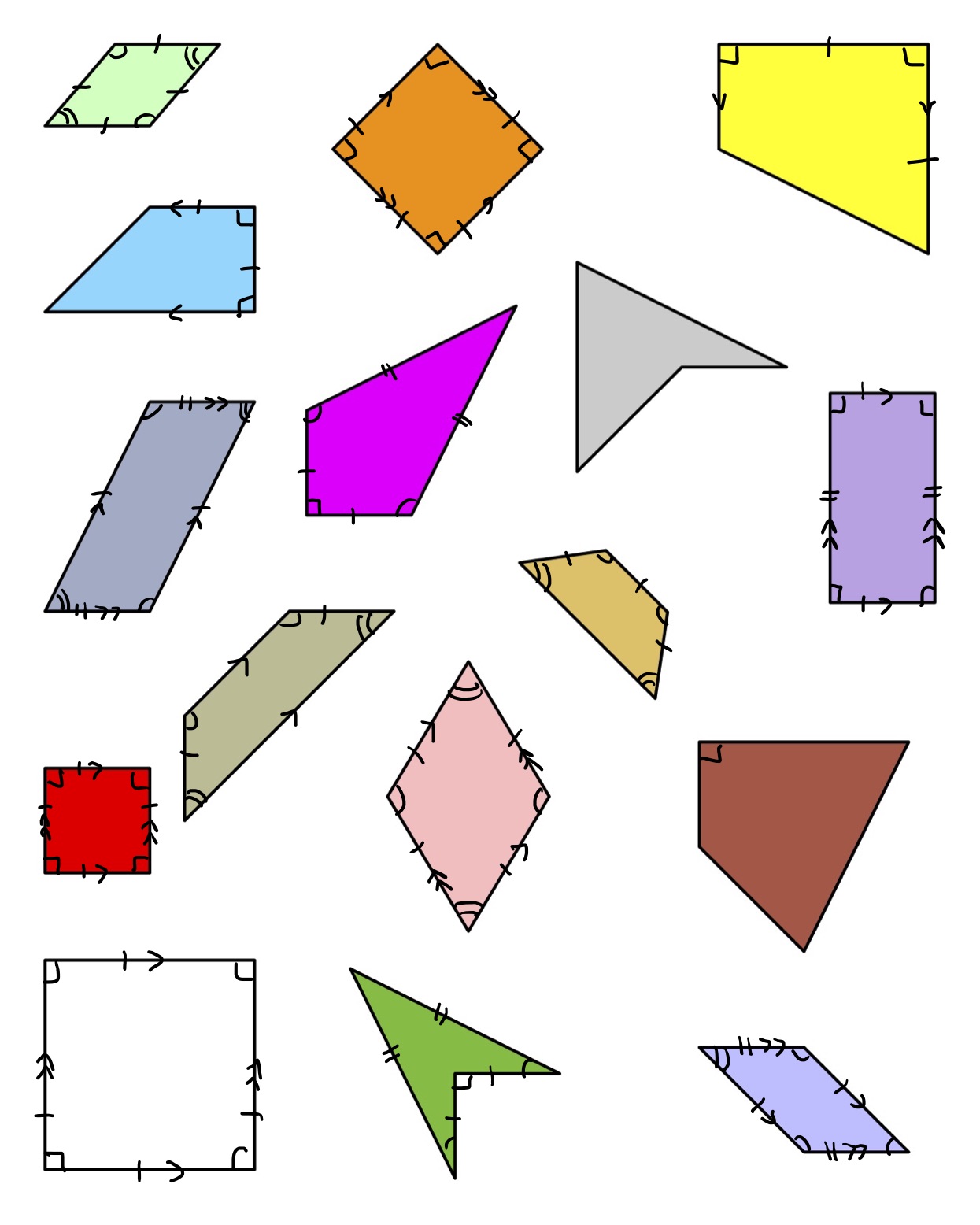
2. Sorting and mystery definitions
Next we worked on dividing our quadrilaterals into two groups. The items in one group need to have something in common. That property must not present in the items in the other group. An example is below. Can you work it out?
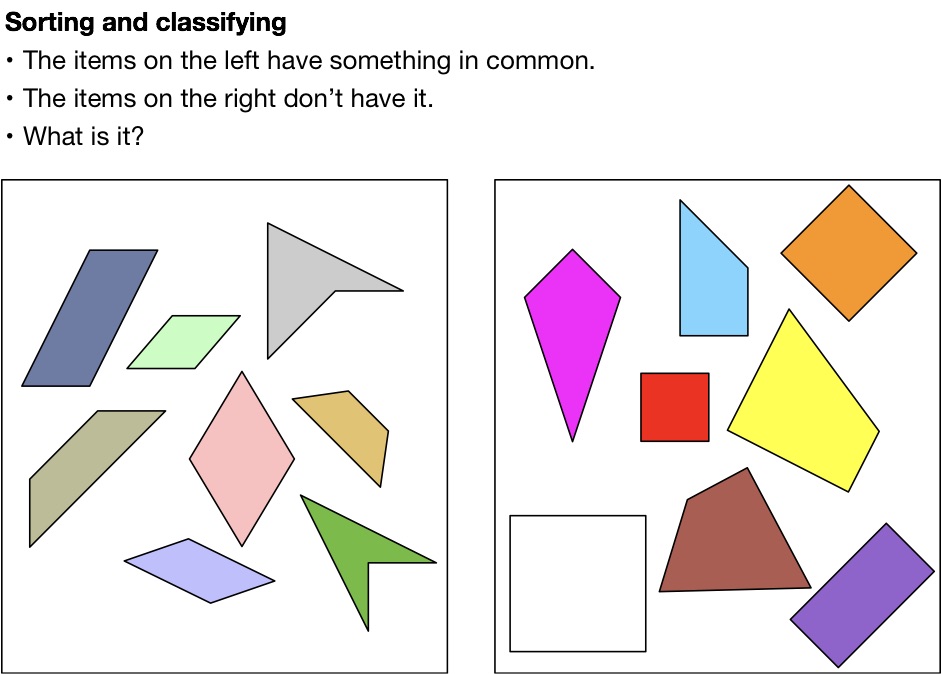
(The items on the left do not have interior right angles. The items on the right do.) I asked students to make up puzzles for each other. This seemed to go well. In retrospect, I should have had a few more examples up my sleeve. I could have also asked them to write theirs down.
3. Guess Who?
We moved into a few rounds of ‘Guess Who?’ with shapes. We reviewed the board game (in the photo above). Key points: each player selects and keeps hidden a mystery person. The other player asks ‘Yes/No’ questions to determine who the mystery person is. We talked about what makes good questions (for example, properties that divide the remaining people as evenly as possible into two groups).
When playing with quadrilaterals, we used sheet protectors (see the photo) to eliminate candidates. This ‘open play’ was also useful in checking each other’s deductions, and in making the game a little more collaborative. This felt successful, though I’d like to listen in a little more closely to some of the conversations.

4. Card/shape sort
To hone in on the nested properties of quadrilaterals, I gave them these cards and asked which properties each of their quadrilaterals had.

Students were able to sort them with relative ease, and so we moved onto the next task.
5. Nested diagrams and family trees
I handed out the following Euler diagram (A3 sized). The task was to put the property cards and the shapes in the relevant regions. We talked about the seven regions, and noted the overlap of the red and the purple. We discussed how an object in the very middle of the diagram has all of the properties and an object at the edge of the diagram (outside the blue ring) has none of the properties.

Some students unintentionally ignored the property cards and made up their own. Few realised that the property cards were numbered in a ‘useful’ way, but I’m not worried about that.
Each region now contains a class of shapes. What are the names of each class of shapes?
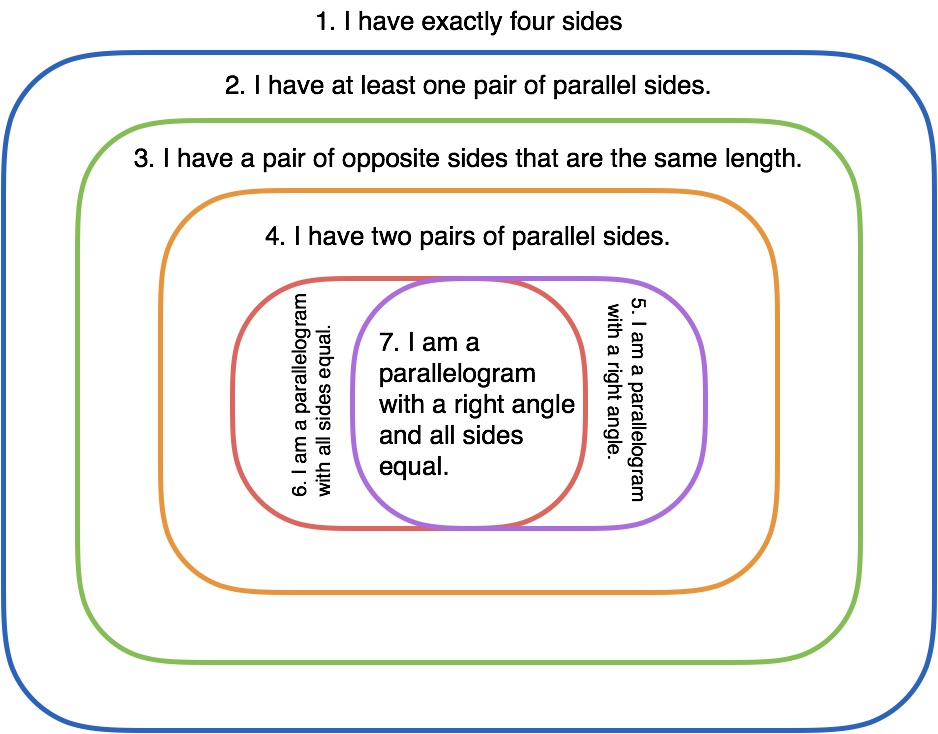
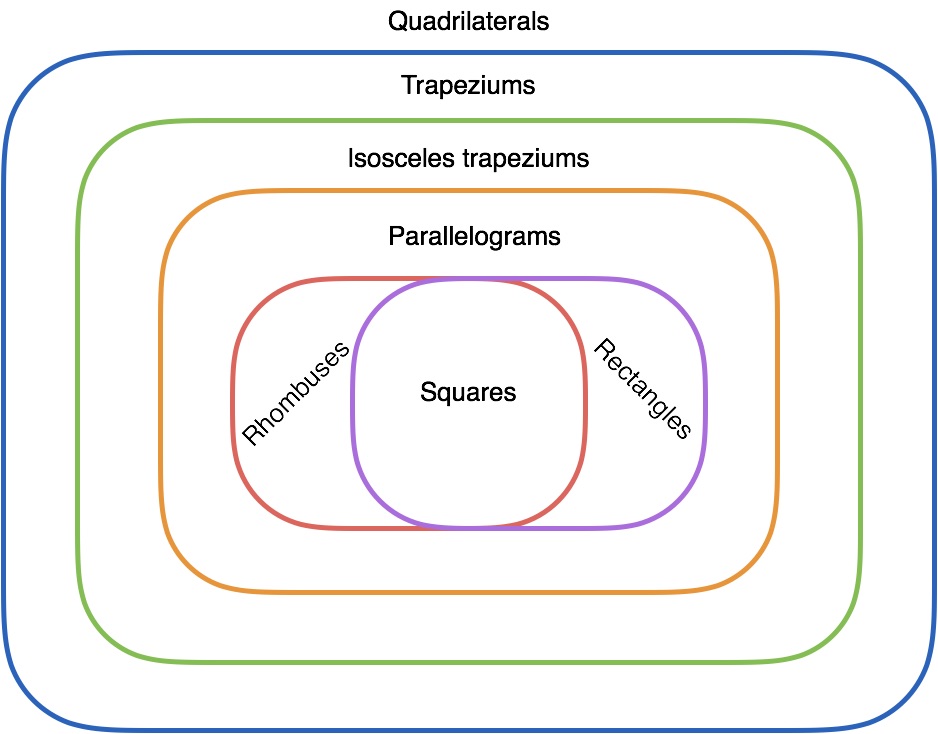
This seemed to come far more quickly. We also connected our nested diagram to a ‘quadrilateral family tree’ (credit to David Butler for his post on this).

Each class of shape inherits the properties of those above it. What I missed here (which is important for what comes next) was nailing down the description of the shapes. What differentiates (say) a kite from a rhombus? As David Butler helped me think about later, what distinguishing features do each class of shapes have?
6. Always, Sometimes, Never True
And finally we come to the troubles … back to claims that are ‘always, sometimes, never’ true.
- A rectangle is a rhombus.
- A rhombus is a rectangle.
- A square is a rectangle.
- A rectangle is a square.
- A parallelogram is a quadrilateral.
- A trapezium is a parallelogram.
- An equilateral quadrilateral is a square.
- A parallelogram is a rectangle.
- An equilateral parallelogram is equiangular.
- A rhombus is a square.
- A square is a rhombus.
- A kite is a square.
- A square is a kite.
I found that it helped to say each statement three times, as follows:
- A rectangle is always a rhombus.
- A rectangle is sometimes a rhombus.
- A rectangle is never a rhombus.
Only one of these can be true. Which is it? If it is sometimes true, then let’s think of examples (and later, properties) where it is true and examples where it is not.
Our problems were with the ‘sometimes’ statements. Consider the statement: ‘A trapezium is a parallelogram.’ As David Butler put it, the answer to a question like ‘When is a trapezium a parallelogram?’ is ‘When it’s a parallelogram’. Not very satisfying!
And ‘not very satisfied’ is a good description of how some students felt. ‘Magic’ is probably what others thought; I think they viewed it as redefining what it meant to be ‘a trapezium’ or ‘a parallelogram’.
Now I wonder if it is helpful instead to start considering ‘sometimes’ statements by first leaning heavily on their definitions and then looking for distinguishing features of isn’t and is.
For example, consider the statement ‘A rectangle is a rhombus’, which we agree is sometimes true. Let’s review our definitions:
- A rectangle is has two pairs of parallel sides and angles that are 90 degrees.
- A rhombus has two pairs of parallel sides and all sides are the same length.
So, when isn’t a rectangle a rhombus? When the pairs of opposite sides of the rectangle are of different lengths. When is a rectangle a rhombus? When all sides are of the same length. If we add this condition to our definition of a rectangle then, to be a rhombus, our rectangle must have two pairs of parallel sides, right angles, and all sides of equal length. (Note that I’ve just described a square, so a rectangle is a rhombus when the rectangle is a square.)
And now what?
I’ve written about 1700 words to discover that most of what happened today seems okay, but could be tweaked. So in tomorrow’s repeat of this workshop, I’ll include definitions of these quadrilaterals and I’ll reframe the ‘sometimes’ statements as I outlined above. Also, when naming shapes, I’ll use the prompt ‘What is the most precise name that we can give this shape?’ Finally, I’ll try to articulate more clearly the role of these activities in ‘developing (our) mathematical thinking’ — the whole point of the course.
I’ll report back with an addendum to this post to see whether any of these ideas help it go smoother.


Lovely! The emphasis on reasoning and generalization is so nice. The idea of the record sheet having multiple uses and keeping track of what properties you find is cool. Several great activities, but it feels like you wove them into a cohesive whole.
A couple things I do that might or might not fit in. For elementary teachers, I think a lot of the work for learners is going from visual (van Hiele 0) to property (vH 1) reasoning. So we start with making quadrilaterals on GeoBoards and describing to someone to try to get them to make it to uncover some of the properties. The goofiest thing I do is slides from my quadrilateral vacation (https://www.slideshare.net/goldenj/my-quadrilateral-vacation2010) to get at our theme of variety of examples.
LikeLike
I loved the post. Such a mix of ideas that seemed more successful than perhaps you initially thought. I wonder what students think?
I liked your question: what’s the most precise name we can give this shape?
It made me try and think of another way to phrase the question about trapeziums and parallelograms. They sound a bit like dad jokes.
eg What do you call a trapezium with two sets of parallel sides? A: a parallelogram.
Here’s some more:
What do you call a trapezium with two sets of parallel sides and a right angle?
What do you call a trapezium with 3 right angles?
What do you call a trapezium with two sets of parallel sides, a right angle and 2 adjacent sides of equal length?
What do you call a quadrilateral with 2 right angles and only one set of parallel sides?
As I wrote these I tried to think about the minimum info needed. It made me realise:
* that I could focus on different attributes but that some determined others.
* that there were multiple ways I could describe a shape.
* that there’s another attribute I relied on: internal angle sum of a quadrilateral is always 360 degrees.
I love that your blog post made me think differently about how I could approach teaching this. Thanks!
LikeLike
Amie, I love how you have developed this task).
This was a new activity for me, and Kath will tell you, I felt exactly the same as you did. You could have used me as the visual.
I like the connection you made to claims and the conceptual build in your overview is logical and creative.
When I read dot point 6, Sometimes Never Always, I could anticipate some confusion due to the common misconceptions learners have.
My quick thinking is:
How about an activity something like …you get dealt a number of the Property cards and you have to draw a shape that satisfies all properties. It might be that you are in a pair and each of you pick one card. Both of you draw a shape that satisfies both cards without consulting and then compare and discuss. This could also work for bigger groups. It is a fluency task but might be a quick consolidation before you move onto the more complex considerations.
Thanks for sharing. I was 50-50 about using the task again but I will definitely do that now.
LikeLike