School maths
I have always loved maths, but the reasons why have changed dramatically over time.
This is my Year 1 work. It reminds me about what I thought it meant to be good at maths: lots of ticks on neat work, especially if it was done quickly.

This attitude was reinforced by my report cards in primary school. A typical one looks like this. Note the focus on speed and accuracy. I loved maths because I was good at it.

Our Year 2 classroom had a corner filled with self-directed puzzle-type problems. If students finished their work early, they could go to the puzzle corner. I recall spending a lot of time there (my report says I was put in an extension group). Looking back, I’m sad that not every student had the same opportunities to engage with these richer, stimulating problems.
Outside of school, I loved doing and making up puzzles. I looked for patterns everywhere. I was always thinking about different ways to count, to organise, and to get things done more quickly. Growing up on a rural property, I had a lot of chores and time to think. For example, I’d think about how many buckets of oranges I could pick in an hour, how long it would take us to fill an orange picking bin, the different ways I could climb the rungs of the ladder, and so on. But I didn’t connect these ideas to maths.
Most of my school maths memories involve doing exercise after exercise from the textbook, but that was fine by me because I could put a self-satisfied tick next to each neatly done problem (after checking the answer in the back of the book!). I remember one high-school maths project to work out the most efficient way to wrap a Kit Kat in foil. It stands out in my memory because it was so different to the rest of maths class.
There were gaps in my knowledge along the way that I tried to cover up. I missed a month of Year 4 due to illness, and a substantial chunk of that time was devoted to fractions. When I got to algebraic fractions in later years, I would furtively use my calculator on simple examples to see if I could work out the right ‘rule’. Now I congratulate myself on having the sense to work it out for myself by generalising from specific examples. In Year 12 I felt embarrassed for using straws and Blu Tack to make visualisations of 3D coordinate geometry; everyone else could do it in their heads. Now I’m proud that I found a tool to help me make sense of the maths.
In Year 12 I hit a big obstacle. All my grades went downhill, including in maths. My maths report card says that I was ‘prone to panic attacks when working against a time constraint’. I don’t remember that, although I do remember crying (which I almost never do) in my maths teacher’s office and thinking that I didn’t know anything. I realise now that much of my maths schooling was about memorisation but not about understanding, and that it had caught up with me by Year 12.
Despite my mostly mediocre grades (I got a D in physics!), I did okay and was offered several university places. My love of the English language drew me to careers such as law, journalism and psychology. But I had also applied for and been offered a place in mathematics. Despite this, I chose to repeat Year 12. I took maths again because I still enjoyed it. The second time around it seemed to make a lot more sense; my scores were 19 and 19.5 for Maths 1 and 2. At the end of Year 13 I was awarded one of the first UniSA Hypatia Scholarships for Mathematically Talented Women. This boosted my confidence and made University study more affordable for a country kid. So, I decided to do mathematics. I also enrolled in a computer science major because I wasn’t sure what kind of job you could get with a maths degree.
University days
Most of my undergraduate mathematics experience was the same as high school. I got Distinctions or High Distinctions for all my subjects (except Statistics 3B where I scraped a pass). I did most of my thinking in my head and then committed it to paper. I produced beautiful notes, and would rewrite a page if it had a single mistake on it. On reflection, I had a fairly superficial understanding of mathematics, but knew what to do to get good marks. I got disenchanted in the third year of my four-year degree and briefly considered quitting, but I had never quit something so important so I kept going.
At the end of third year, I had an experience that made me sure I wanted to be a mathematician. I attended a Mathematics-in-Industry Study Group. This is a five-day event that draws together around 100 mathematicians. On the first day, we listen to five or six different companies tell us about a problem they have that needs solving. For example, they might say ‘we want to stop washing machines from walking across the floor when they are unbalanced’ or ‘we want to know the best way to pack apples in cartons’. The mathematicians then decide which problem they want to work on, and smaller groups spend the next three and a half days feverishly trying to find a solution.
It was transformative as I witnessed, first-hand, mathematics put into action. I also saw how mathematicians creatively and collaboratively approach solving problems. I watched accomplished mathematicians initially not know how to start. I saw them making mistakes. They had intense (but friendly) discussions about whether something was the right approach. It was a defining moment, because it showed me how mathematics is really done, beyond learning mathematics that’s already known, or applying algorithms without a sense of why we would do so. I saw the true habits of mathematicians in action. I also discovered the important role that communication plays in mathematics, and that I could put my love of the English language to good use.
The transition from doing maths exercises with answers that were ‘perfect’ the first time to the more authentic and messy problem-solving required for mathematical research was not an easy one for me. I found it difficult in my PhD to accept that I was not perfect and that I had to constantly draft and refine both my mathematical ideas and my writing, especially because I had never been taught these skills. But I was helped in being surrounded by more experienced mathematicians who modelled, if not explicitly articulated, that this was how mathematicians really work.
It’s eight years since I was awarded my PhD, and I can now say that I am quite comfortable with this ‘messy’ approach to maths. I like to say that mathematicians are chronically lost and confused, and that is how it is supposed to be. It would be ridiculous for mathematicians to spend their days solving problems that they already know how to solve. So, being uncertain about whether something will work, or uncertain about what to do next, is a natural way for mathematicians to be.
Teaching maths
I started teaching mathematics during my PhD. At first I taught exactly as I had been taught, with procedures and algorithms. But I also didn’t want to respond to a student with ‘Because that’s the rule’, so I started trying to really understand why maths concepts worked the way they did. I learned so much more about maths when I started to explain it to others. The way I taught expanded to include visual ways to think about maths, a variety of representations and approaches, and other flexible ways of thinking. It wasn’t natural to me at first (and at times I still solve arithmetical problems in my head by imagining a pen writing the algorithm) but it has immeasurably enriched my own understanding of mathematical concepts.
I also realised that the way I was taught was not the way I wanted to teach, but I wasn’t sure how to change that. I sought ideas from the internet, and eventually stumbled into the early days of the online community that is the MTBoS (the Math Twitter Blogosphere), although I didn’t realise that until much later. I lurked for a long time because I felt like an outsider: I wasn’t a school teacher (what did I know about education?!) and I wasn’t located in North America. Today I couldn’t imagine teaching without the support of my professional community on Twitter which extends all around the world.
Around five years ago I decided that I could help break the cycle of traditional procedural-based teaching by supporting students, particularly preservice teachers, in experiencing maths in the ways that I and other professional mathematicians do. So, I designed a course that gives students these problem-solving experiences alongside learning skills for thinking and working mathematically. I hold these word clouds from Tracy Zager in my head as a reminder and a motivation of what I am trying to accomplish. (You can read more about how I found them here.)
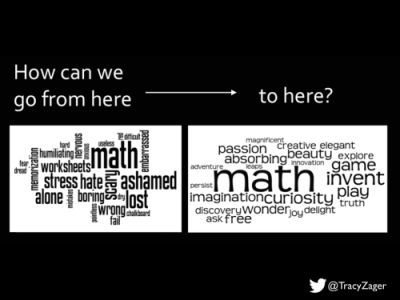
I still love ‘cracking puzzles’ in maths like I did in Year 2, but my love of maths has expanded to include learning how others think about mathematical ideas. In almost every class I see a student think about a problem in a way I’d never imagined, and I love it. Listening to student thinking is why I’ll never tire of teaching, and it helps me to be a better teacher. I can’t wait to learn from you.

You are an inspiration Amie – I love that you have shared your journey. It gives me confidence to continue to pursue your approach to teaching mathematics in my role as a mathematics teacher to young people.
LikeLike
Thanks Vanessa. It’s my respect for the work that you and your colleagues do that made me realise I have to learn a lot more about school teaching. So I’m about to start a Master of Teaching. Wish me luck!
I’m inspired about what we can do as a community when we work together. I’ve read a lot of maths autobiographies recently, and they almost all talk about procedurally-based classrooms. But I hope we are making an impact. I can’t wait to read the maths autobiographies of our students!
LikeLike
Thanks for this Amie. My journey in maths has similarities to yours. Unlike you it was not events within the research community that lead me to a transformative experience, rather it was conversations with a mathematics educator that brought things together.
I was capable at what I was asked to do at school. And I certainly remember speed and accuracy being rewarded there. University was more of the same and looking back I learnt how to do well, without any deep understanding. I did get frustrated at the assessment and got a sense that exams were a speed contest, not an opportunity to show deep understanding.
Unfortunately for me I feel as though my honours and postgraduate years were so overly scaffolded that even then I didn’t really learn what it is to do mathematics. No disrespect at all to my supervisor who is one Australia’s finest applied mathematicians – I know he thought he was doing his best by me. At the time, I thought his approach to my “research” internship was entirely appropriate, because it was like my undergraduate years. Looking back I wish he wasn’t so attentive and had me work out things for myself.
I finished my PhD in three years and three weeks and the following day took up my lecturing job in north QLD. This was 1993. I had moved to a department in decline and there was no broad culture of research or doing of mathematics. The most authentic doers of mathematics were actually the physicists on the floor below, but it took me a while to work this out. It was very much a place where we did direct teaching in the way I had experienced as a student.
By 2007 I was in a multi-disciplinary school and my responsibilities extended outside of mathematics into physics and assisting with off-shore delivery of IT. Somehow my efforts in teaching were recognised and I got approached to take a leadership role in the science faculty. It was a role where I had no power. I was supposed to use my “influence” to raise the profile of teaching. This did give me an opportunity to reflect – not on mathematics, but on what we were doing in our BSc – and I decided to focus on numeracy, because I knew this was an issue frequently discussed by the cohort of academics. I got to mix with other learning and teaching people across Australia and be involved in some great projects.
In 2010 I decided I needed some help from somebody with a knowledge of education, because I wanted to formalise some of the work I had been doing. I ended up meeting the mathematics educator, Jo Balatti. I did not ask for her. This was the person the Head of Education got me to meet.
It did not take long before Jo started telling me about her struggles with the maths pedagogy subject. She very quickly got me to realise that I as a mathematician had a responsibility to focus on the cohort of preservice maths teachers. There was a lot of distrust between education and the sciences and maths within the university, so there was not a history of cooperation. But Jo pointed out to me that her students were doing at least four subjects of maths in my discipline before she begins to teach them maths pedagogy in education – and that her experience was these students were very weak when it came to explaining mathematics concepts and procedures.
My interactions with Jo lead to a lot of reflection by me about mathematics and the way it needs to be taught. This is not to say that I had not contemplated this before. Despite my own lack of profile in research mathematics I knew enough from the conference circuit that mathematics is a very powerful bunch of knowledge and pursuits in mathematics are not procedural in nature. However it was not until I thought about Jo’s words that I really began to understand how our approaches in maths teaching were unhelpful.
Jo & I co-wrote a subject for preservice maths teachers – and this subject has given me an opportunity to revisit so much of mathematics – in a way that we hope helps aspiring maths teachers to do a good job. And I agree with the message in the word clouds of Tracy Zager – that there is so much to the body of knowledge we call mathematics that we ought to get across. This includes the messiness of problem solving and the absolute thrill of the light-bulb moments where connections are made and the beauty of the structures within mathematics are revealed.
LikeLike